Corresponde a una figura geométrica tridimensional, es decir, que se proyecta en tres dimensiones: largo, ancho y alto. Debido a esta característica existen en el espacio pero se hallan limitados por una o varias superficies.
Si todas las superficies que lo limitan son planas y de contorno poligonal, el cuerpo es un poliedro.
Los poliedros se clasifican en regulares e irregulares.
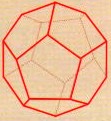 |
Poliedros regulares, son aquellos cuyas caras son todas polígonos regulares, congruentes entre sí (de igual medida) y cuyos ángulos poliedros son iguales. Existen solamente 5 poliedros regulares: Tetraedro, Hexaedro, Octaedro, Dodecaedro,Icosaedro.
Para los geómetras griegos, el estudio de los poliedros fue muy importante y conocieron la existencia de esos cinco únicos sólidos regulares, cuyo descubrimiento atribuyeron algunos al propio Pitágoras y a los que Platón recurrió incluso para explicar la creación del universo. Sin embargo, no consta que conocieran un importante resultado relativo al número de vértices, aristas y caras de un poliedro convexo, observado ya por Descartes en 1640 y del que el matemático suizo Leonhard Euler dio una famosa demostración en 1752. Euler demostró que, si se suma el número de caras y el número de vértices de un poliedro convexo y, del valor obtenido, se resta entonces el número de aristas, et resultado es siempre igual a 2. De este resultado, válido para todo poliedro convexo, se deduce fácilmente la existencia de únicamente cinco poliedros regulares.
Tetraedro
|
Hexaedro (cubo)
|
Octaedro
|
Dodecaedro
|
Icosaedro
| |
4 caras (triángulos equiláteros)
|
6 caras (cuadrados)
|
8 caras (triángulos equiláteros)
|
12 caras (pentágonos regulares)
|
20 caras (triángulos equiláteros)
| |
| N° de caras |
4
|
6
|
8
|
12
|
20
|
| N° de vértices |
4
|
8
|
6
|
20
|
12
|
| N° de aristas |
6
|
12
|
12
|
30
|
30
|
| N° de lados de cada cara |
3
|
4
|
3
|
5
|
3
|
| N° aristas concurrentes en un vértice |
3
|
3
|
4
|
3
|
5
|
| Tetraedro regular: está formado por 4 caras triangulares. | 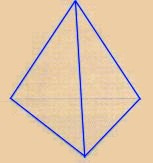 |
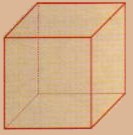 | Hexaedro regular: (cubo): está formado por 6 cuadrados. |
| Octaedro regular: está formado por 8 triángulos equiláteros. | 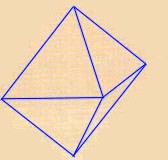 |
 | Dodecaedro regular: lo forman 12 caras pentagonales. |
| Icosaedro regular: está constituida por 20 triángulos equiláteros. | 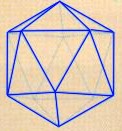 |
Poliedros irregulares: Son aquellos que no tienen sus caras como polígonos regulares ni sus ángulos poliedros iguales.
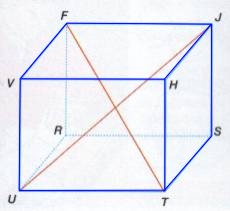 | Prisma: Poliedro limitado por varios paralelogramos y dos polígonos iguales llamados bases, cuyos planos son paralelos. |
| Pirámide: Poliedro que tiene una cara que es un polígono cualquiera al que se llama base y las caras laterales son triángulos que tienen un punto en común llamado vértice. | 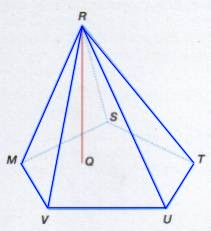 |
Pero hay otros cuerpos, como la esfera, el cilindro o el cono que no están limitados por polígonos, sino por superficies curvas; se llaman cuerpos redondos, que también han recibido desde antiguo una atención especial y cuyas superficies y volúmenes estaban ya estudiados en la obra de Euclides.
Cuerpos redondos: Son los cuerpos limitados, parcial o totalmente, por superficies curvas.
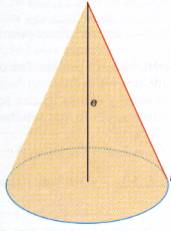 | Cono |
| Esfera | 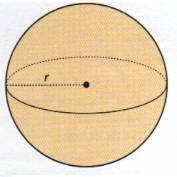 |
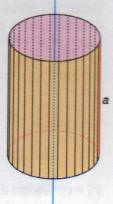 | Cilindro |
Utilidad: La mayoría de los poliedros son figuras que existen en la realidad. Un ejemplo de ellos son las pirámides y los virus.
| Gracias al microscopio electrónico ha sido posible visualizar la estructura de los virus. El cuerpo geométrico que vemos a la derecha es la imagen, realizada por un ordenador, de un adenovirus a partir de la micro grafía obtenida gracias a microscopio electrónico: se trata de un icosaedro, uno de los cinco cuerpos platónicos. | 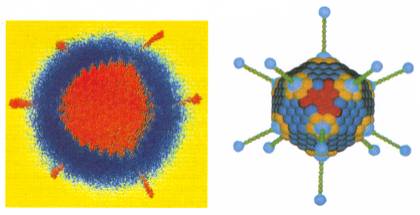 |